Blogs

Understanding Young’s Modulus on Stress-Strain Curves: An In-Depth Tutorial
Introduction
In the realm of material science, understanding the nuances of Young’s Modulus is paramount for engineers and procurement managers alike. This critical parameter not only quantifies a material’s stiffness but also serves as a vital link between stress and strain, influencing decisions that impact safety, performance, and durability.
As engineering applications evolve, the significance of Young’s Modulus becomes increasingly apparent, guiding the selection of materials tailored to specific conditions and requirements. From the rigidity of metals to the flexibility of polymers, the variations in Young’s Modulus across materials illuminate the strategic considerations necessary for optimizing performance in diverse applications.
This article delves into the intricacies of Young’s Modulus, exploring its definition, measurement techniques, and its profound implications in material selection, ultimately equipping professionals with the insights needed to navigate the complexities of modern engineering challenges.
Defining Young’s Modulus: The Foundation of Stress-Strain Analysis
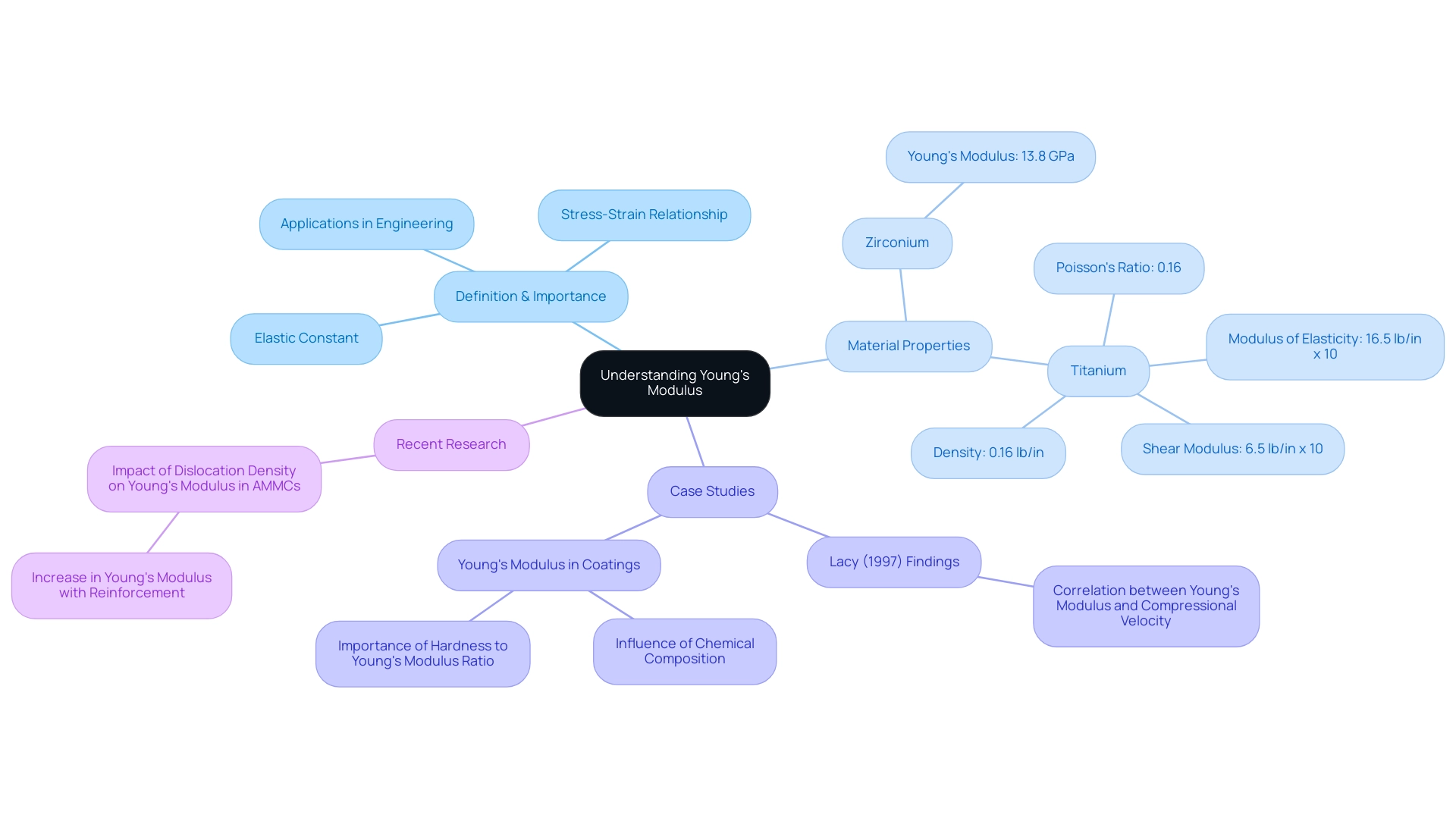
The elastic constant, represented as E, acts as a crucial measure of a solid’s rigidity, playing an essential part in engineering fields. It quantifies the relationship between stress—defined as the force applied per unit area—and strain, which represents the resulting deformation, in the context of Young’s modulus on the stress strain curve. Mathematically, the elastic constant, known as Young’s modulus on the stress strain curve, is expressed as:
E = stress/strain
This crucial attribute, known as Young’s modulus on the stress strain curve, is vital for forecasting substance behavior under different loads, thus assisting engineers and procurement managers in the choice of suitable resources for particular uses. Recent advancements have revealed that:
- The modulus of zirconium (Zr) is approximately 13.8 GPA.
- Titanium exhibits:
- A Modulus of Elasticity of 16.5 lb/in x 10
- A Shear Modulus of 6.5 lb/in x 10
- A Poisson’s Ratio of 0.16
- A Density of 0.16 lb/in
The importance of these values cannot be overstated, as they directly affect the performance and longevity of substances in real-world applications.
Furthermore, Lacy (1997) established a correlation between rock dynamic elastic modulus and compressional velocity through extensive laboratory tests on over 400 core samples from various geological formations in the Gulf of Mexico. This insight highlights the significance of the elastic limit in assessing material performance across various engineering situations. Additionally, a case study on the modulus of elasticity in coatings reveals that the modulus of elasticity of coatings is less dependent on microstructure and morphology but is strongly influenced by chemical composition.
Optimizing the hardness to elastic modulus ratio is crucial for achieving good mechanical performance in high-performance tribological applications. In light of recent research, Madeira et al. observed that the improvement of Young’s modulus on the stress strain curve in Advanced Metal Matrix Composites (AMMCs) with reinforcement substances is mainly due to a rise in dislocation density, emphasizing ongoing progress in the field of science that continues to enhance our comprehension of stress-strain relationships.
Measuring Young’s Modulus: Techniques and Best Practices
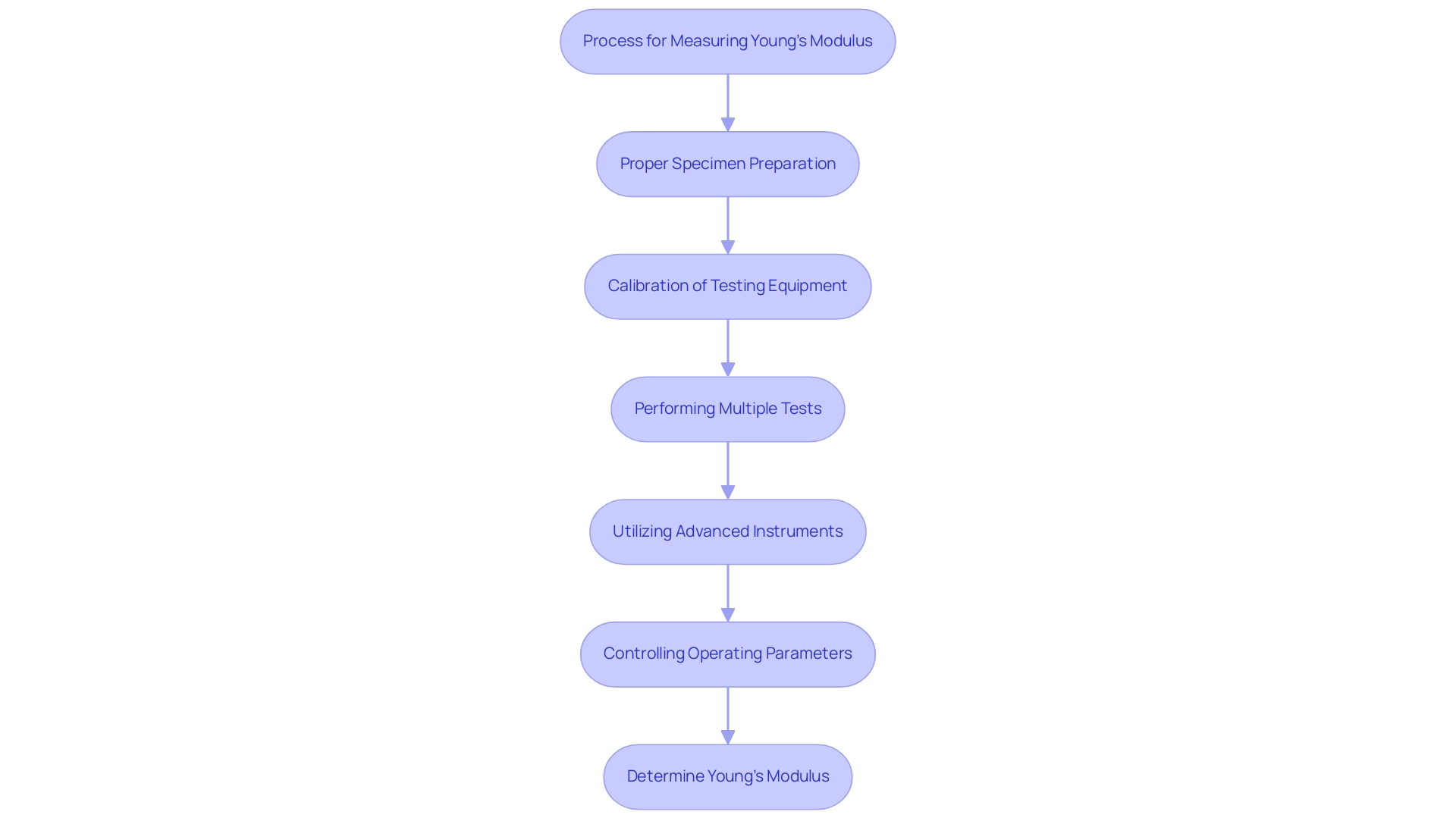
One of the most effective methods for measuring Young’s Modulus is through tensile testing, which involves applying a uniaxial force to a specimen until deformation occurs. This process produces a stress-strain curve from the gathered data, illustrating the substance’s response to stress, which helps in determining Young’s modulus on the stress strain curve. To achieve reliable results, adherence to best practices is crucial.
Key recommendations include:
1. Proper specimen preparation to eliminate potential measurement errors;
2. Calibration of testing equipment, such as a compression load cell with a capacity of 2500 N, prior to each test to guarantee accuracy;
3. Performing multiple tests to mitigate variability in material properties.
Utilizing advanced instruments, like digital extensometers, can greatly improve measurement accuracy, resulting in a more precise assessment of Young’s modulus on the stress strain curve. An illustrative case study titled ‘Significance of Operating Parameters on Elasticity’ highlights how factors like water content and loading rate adversely affect the elastic properties of peanuts.
This highlights the necessity of controlling such parameters to optimize the mechanical properties of substances effectively. Additionally, recent studies have applied a regression model to illustrate the impacts of operating parameters on the elastic modulus, mirroring current trends in the field. As we progress into 2024, utilizing open-source software templates can further streamline the measurement process, offering immediate applicability and adaptability across various devices.
As noted by E.D., the collaborative efforts of the research team, including contributions from J.N., J.C.A., and N.L., emphasize the importance of a comprehensive approach to understanding these properties.
The Importance of Young’s Modulus in Material Science
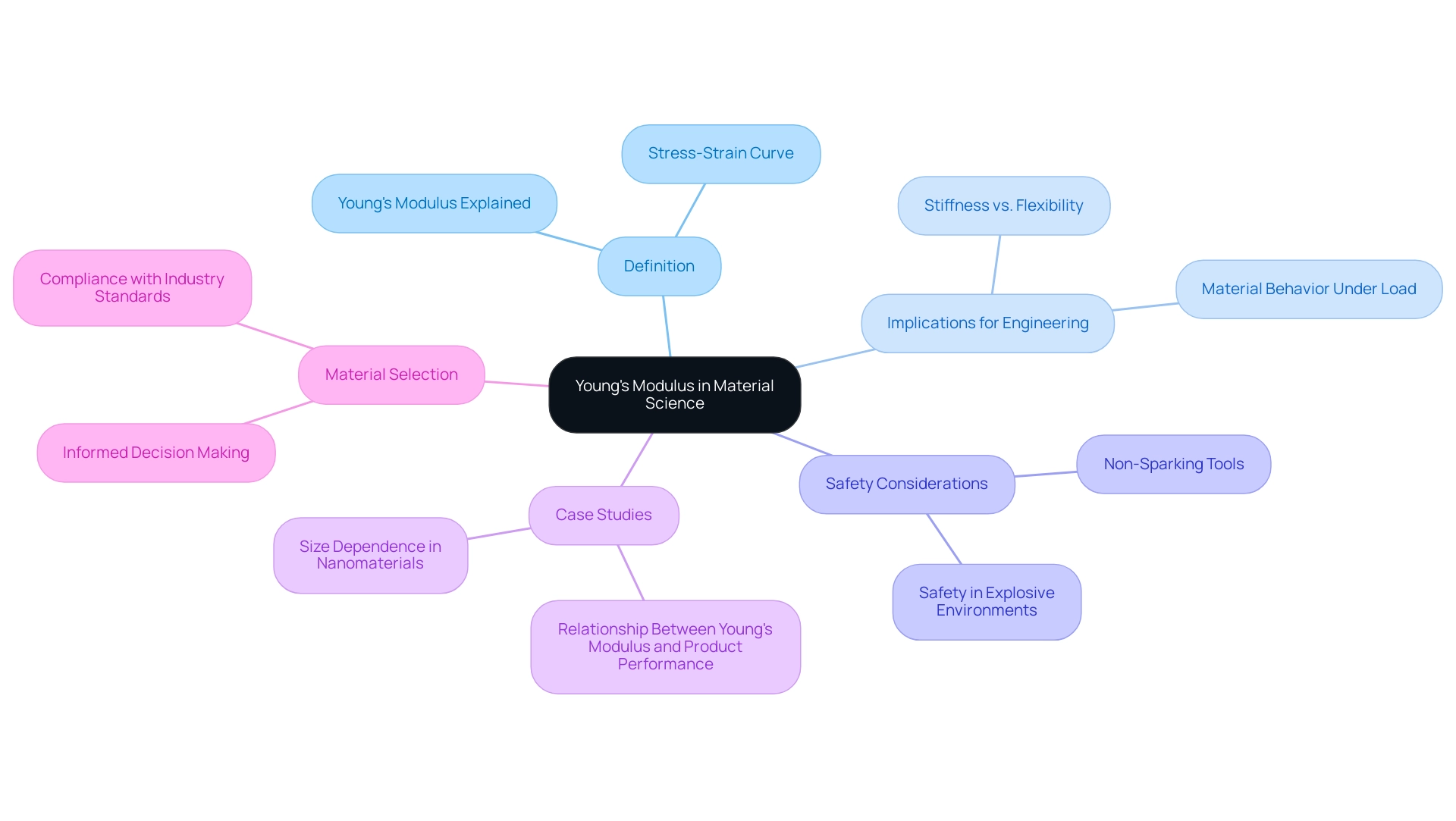
Young’s modulus on stress strain curve is a crucial factor in comprehending substance behavior under stress, directly affecting engineering choices, especially in explosive settings where safety is essential. A high elastic modulus indicates a substance’s stiffness, rendering it appropriate for structural uses that require rigidity and stability. On the other hand, substances showing reduced elasticity values provide increased flexibility, beneficial in uses needing stretchability.
According to Mallory McGuinness-Hickey, because the young’s modulus on stress strain curve directly influences a polymer’s behavior under various loads and stresses, engineers can make informed choices about selection. This insight is crucial for procurement managers to grasp these mechanical properties to ensure that the materials chosen not only align with performance criteria but also comply with relevant industry standards. In explosive environments, Non-Sparking Tools are the best alternative for non-sparking uses, as they provide the necessary safety without compromising performance.
Recent studies have shown that the modulus of elasticity of the pore wall increased by 0.60% with 0.5 MPa CO injection, highlighting quantitative changes under specific conditions. Furthermore, the consistent focus on sensing the power of substances highlights the significance of grasping their characteristics in real-world uses. A significant case study titled ‘Relationship Between Young’s Modulus on Stress Strain Curve and Product Performance’ demonstrates how the young’s modulus on stress strain curve directly impacts a polymer’s behavior under loads and stresses, affecting selection and design for safety and reliability.
Such knowledge is instrumental in guiding the selection of resources, including Non-Sparking Tools, that meet safety and reliability requirements across diverse applications, thereby fostering innovative solutions tailored to specific engineering challenges.
Young’s Modulus and Its Relationship with Material Properties
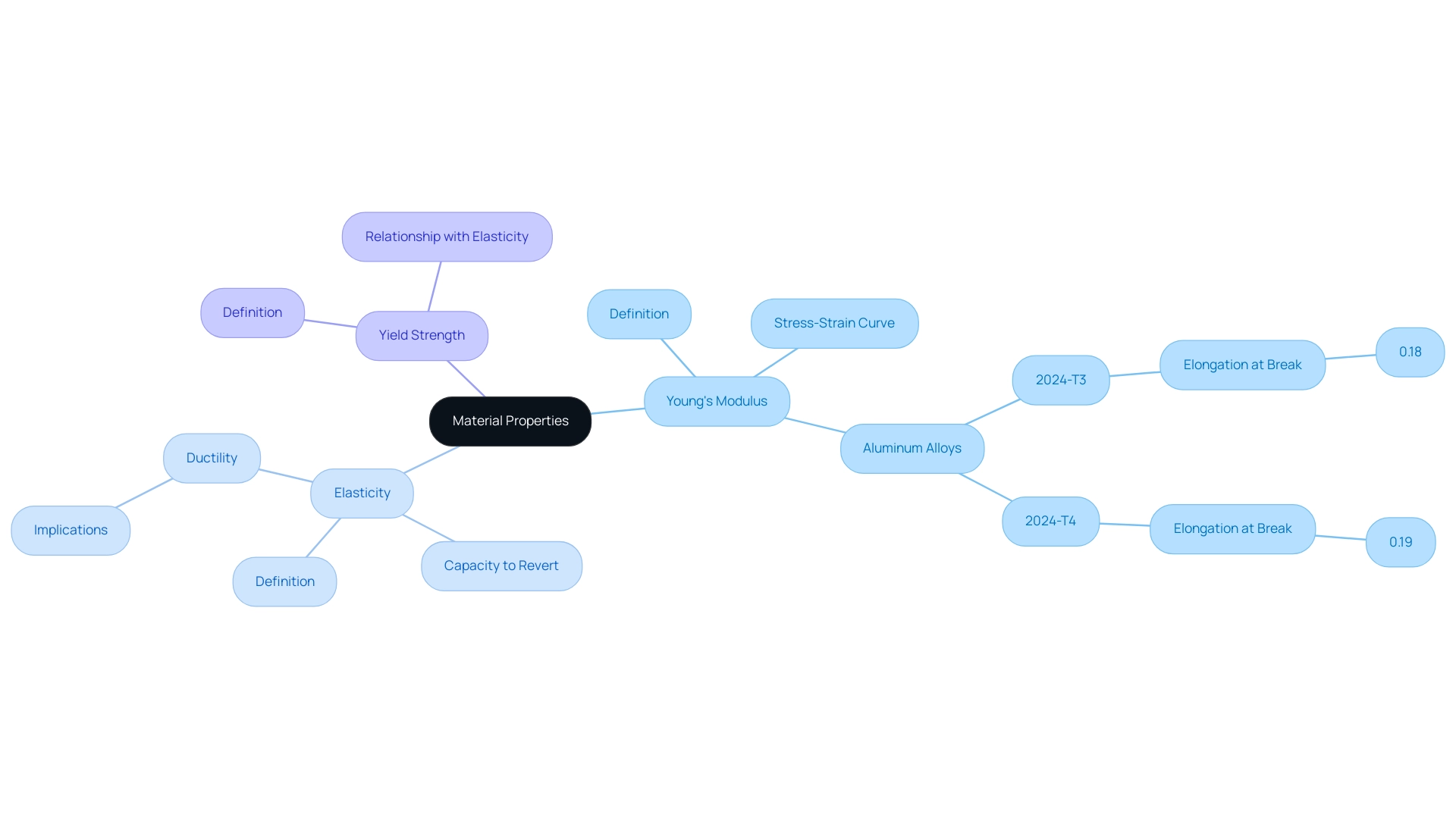
The elasticity constant functions as a fundamental parameter that intricately links various properties such as the young’s modulus on stress strain curve and yield strength. Elasticity defines a substance’s capacity to revert to its original form following deformation, while the young’s modulus on stress strain curve indicates the maximum stress a substance can endure before undergoing permanent deformation. Typically, substances showing a greater elasticity also reveal increased yield strengths, rendering them excellent choices for load-supporting uses.
In contrast, those with a lower elasticity often exhibit greater ductility, allowing them to absorb substantial energy without breaking. This interplay is particularly pronounced in aluminum alloys, such as the 2024 series, which maintains a consistent density of 2.78 g/cc across different tempers. Notably, the elongation at break for 2024-T3 is recorded at 0.18, while 2024-T4 exhibits a slightly higher value of 0.19.
Comprehending these relationships is crucial for procurement managers to make informed choices when selecting resources for specific applications. Recent research from the Australian Research Council highlights how external stress and creep aging temperature influence hardness and precipitation processes in 2024-T3 aluminum alloy. The study found that the precipitation process is sensitive to external stress and aging temperature, with specific temperatures identified for under aging, peak aging, and over aging.
Such findings confirm that the connection between the elastic modulus and yield strength, particularly in relation to young’s modulus on stress strain curve, is not just theoretical but has concrete implications for performance and selection. The authors gratefully acknowledge the Australian Research Council (ARC) for supporting this work through the ARC Center of Excellence for Design in Light Metals.
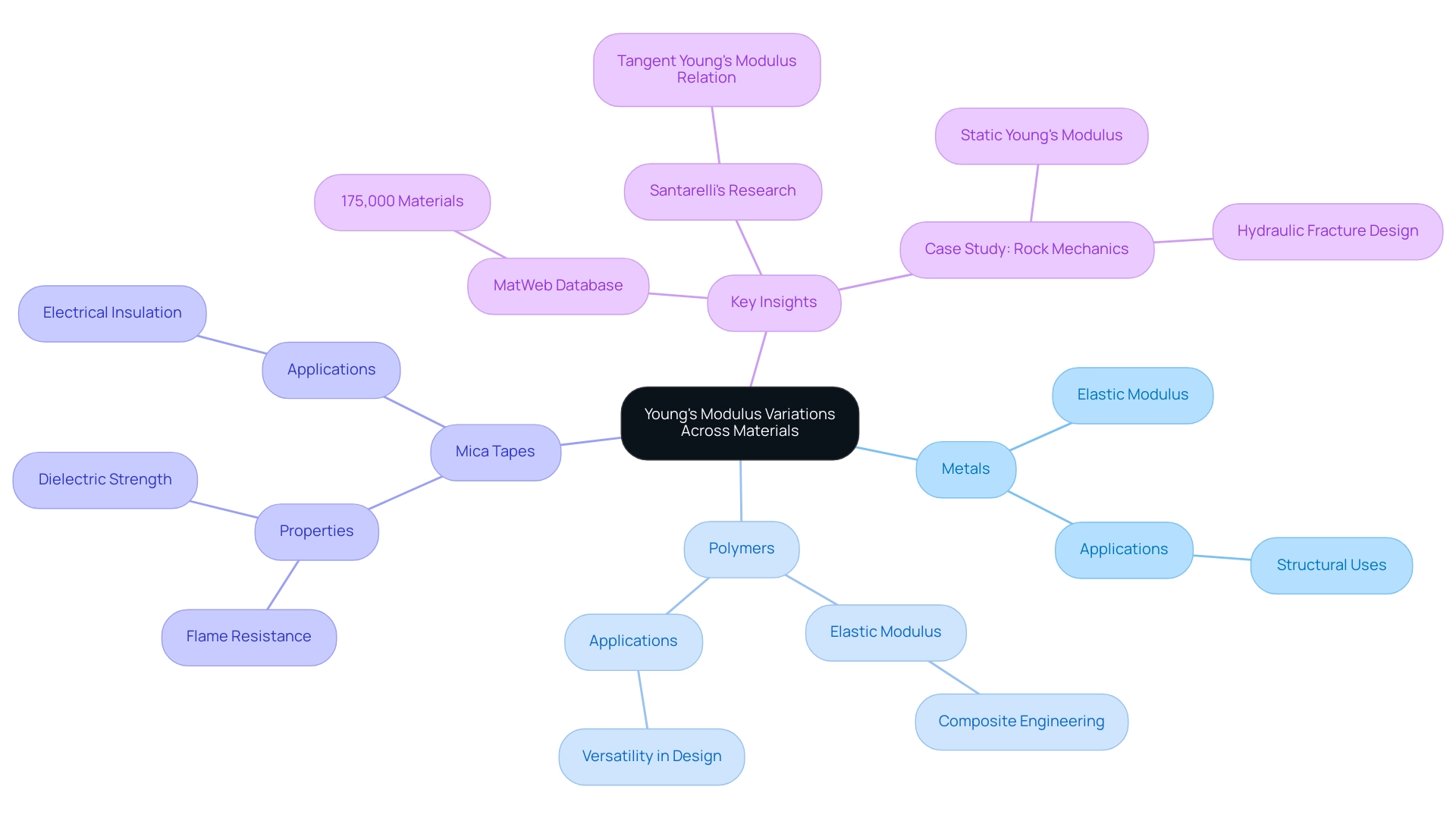
Exploring Variations of Young’s Modulus Across Materials
The differences in elastic modulus among various substances are substantial and affected by numerous factors, such as composition, temperature, and processing techniques. Generally, metals exhibit higher young’s modulus on stress strain curve values compared to polymers, rendering them more suitable for structural uses where rigidity and strength are paramount. In the context of procurement, materials such as Domadia’s Mica Tapes, created for high-temperature resistance and electrical insulation, illustrate how understanding mechanical properties directly affects safety and performance in crucial uses.
Notably, these mica tapes provide excellent flame resistance and dielectric strength, making them essential for electrical uses that require enhanced safety measures against fire hazards. Additionally, the importance of Non-Sparking Tools in explosive environments cannot be overstated, as they provide a safe alternative for non-sparking applications, ensuring reliability in hazardous conditions. Santarelli’s research indicates that the tangent modulus at 50% peak strength can be reliably represented by specific relations, underscoring the nuanced understanding required in selection.
Furthermore, MatWeb offers an extensive database of engineering properties for over 175,000 substances, serving as a valuable resource for procurement professionals evaluating performance. On the other hand, polymers, although usually displaying reduced stiffness, can be enhanced through composite engineering to reach targeted elastic values, offering versatility in design and use. This adaptability is crucial for procurement managers who must assess resources not only for performance but also for cost-efficiency.
Grasping the differences in the elasticity of substances is crucial as it guides choices concerning the appropriateness of resources in diverse uses, from building to sophisticated manufacturing methods. For instance, the case study on the young’s modulus on stress strain curve in Rock Mechanics illustrates how static Young’s modulus is vital for in-situ stress analysis and hydraulic fracture design, emphasizing the practical implications of these material properties. Overall, the diverse applications of mica tapes across industries highlight their versatility and the critical role they play in ensuring safety and performance in electrical insulation.
Conclusion
Understanding Young’s Modulus is crucial for professionals in material science and engineering, as it serves as a foundational parameter that informs the selection and application of materials across various domains. This article has explored the definition of Young’s Modulus, its measurement techniques, and its significant implications in material selection, highlighting the direct relationship between stiffness, elasticity, and yield strength.
The variations in Young’s Modulus among materials, from metals to polymers, underscore the importance of tailored approaches in engineering applications. Factors such as composition, processing methods, and environmental conditions play pivotal roles in determining the mechanical properties of materials. As illustrated through case studies and recent research findings, the insights gained from understanding Young’s Modulus can lead to improved safety, performance, and reliability in critical applications, particularly in environments where material behavior is paramount.
Procurement managers and engineers are encouraged to leverage this knowledge to make informed decisions that align with both performance criteria and industry standards. By recognizing the strategic importance of Young’s Modulus, professionals can enhance their material selection processes, ultimately driving innovation and ensuring that engineering solutions meet the evolving challenges of modern applications.




