Blogs

How to Calculate Young’s Modulus from a Stress-Strain Curve: A Step-by-Step Guide
Introduction
In the realm of engineering and materials science, understanding the nuances of Young’s Modulus is paramount. As a fundamental measure of a material’s stiffness, it plays a critical role in predicting how materials will behave under stress and strain, enabling engineers to make informed decisions about material selection and design. From the automotive industry to electronics, the implications of Young’s Modulus extend far beyond theoretical calculations; they directly influence the durability and functionality of components vital to performance and safety.
This article delves into the definition, calculation methods, and applications of Young’s Modulus, providing a comprehensive overview that equips procurement managers and engineers with the insights necessary to navigate the complexities of material properties in their projects.
Understanding Young’s Modulus: Definition and Importance
Understanding how to calculate Young’s modulus from a stress strain curve is essential, as the elastic modulus, often known as Young’s modulus, acts as an important indicator of a substance’s rigidity. This property quantifies how to calculate Young’s modulus from a stress strain curve, which defines the relationship between stress—defined as force per unit area—and strain, representing the deformation an object undergoes in response to stress, all within the elastic limit of the object. Understanding how to calculate Young’s modulus from a stress strain curve is crucial for engineers and substances researchers as it allows them to anticipate the behavior of items under stress.
This predictive capability is particularly crucial in the automotive and electronics sectors, where the performance and reliability of components are paramount. For example, the choice of substances with the suitable elasticity can greatly affect the longevity and effectiveness of automotive components and electronic gadgets, guaranteeing they satisfy strict performance standards in practical uses. Recent lab tests have demonstrated a relationship between dynamic elasticity and compressional velocity, quantified at 0.265 and 2.04.
Additionally, Lacy (1997) obtained significant insights from over 400 core samples of different rock types, demonstrating the importance of elasticity in geological substances. Additionally, a case study on elastic modulus data for alloys such as Ti-6Al-4V, Inconel IN718, and AISI 316L illustrates how to calculate Young’s modulus from a stress strain curve, emphasizing the temperature-dependent elastic properties and practical implications in both additive and conventional manufacturing processes.
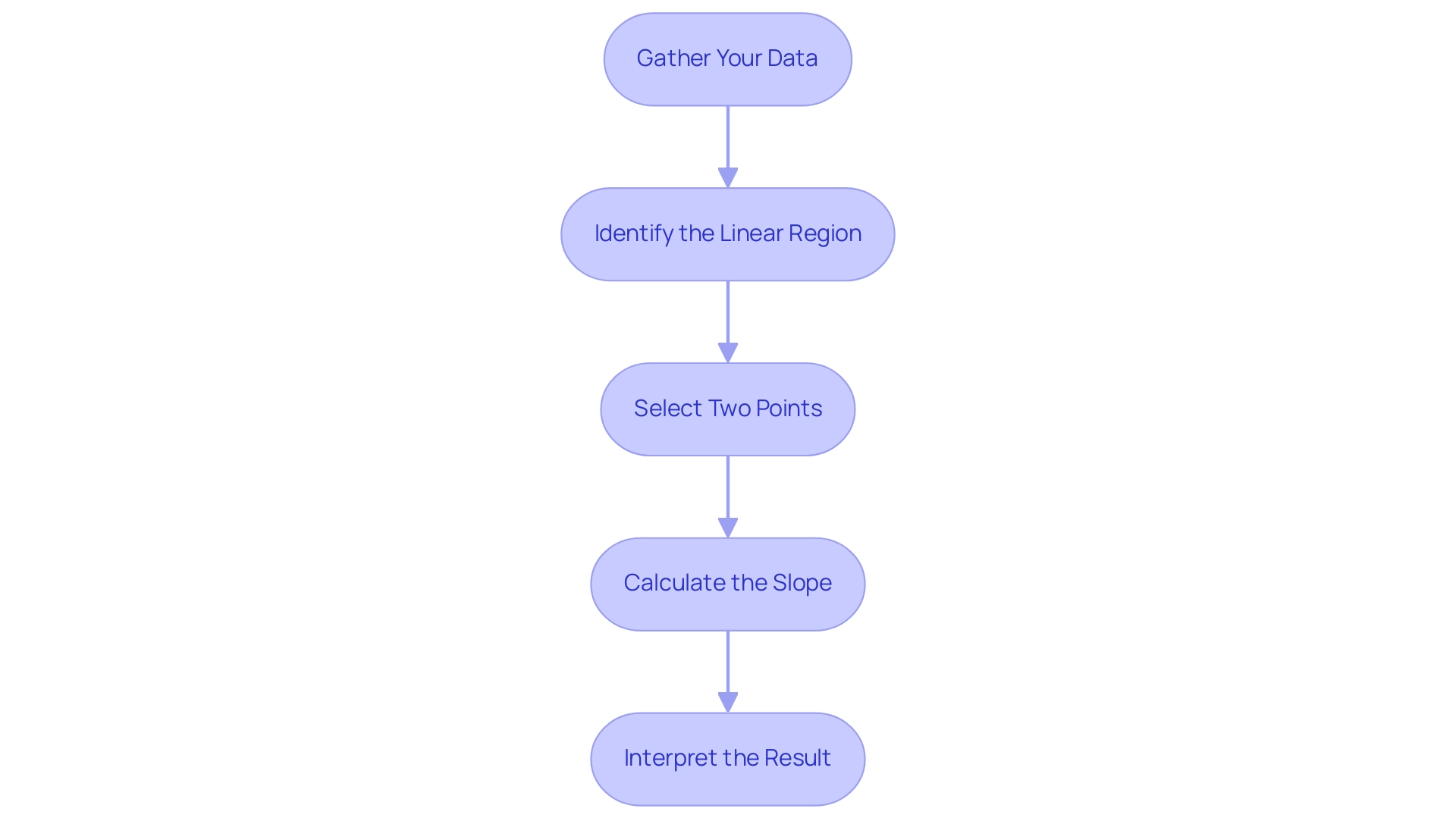
Step-by-Step Guide to Calculating Young’s Modulus from a Stress-Strain Curve
Gather Your Data: Begin by obtaining the stress-strain curve derived from your testing experiment, typically produced through tensile tests. This curve offers essential insights into the substance’s mechanical behavior.
Identify the Linear Region: Focus on the initial linear segment of the stress-strain curve, where the substance exhibits elastic behavior. This area is essential for precisely ascertaining Modulus.
Select Two Points: From the linear portion of the curve, select two distinct points to facilitate your calculations. For example, point A may correspond to (stress, strain 1), and point B to (stress, strain 2).
Calculate the Slope: Employ the slope formula for Young’s Modulus:
Young's Modulus (E) = \frac{\Delta \text{stress}}{\Delta \text{strain}} = \frac{\text{stress2} - \text{stress1}}{\text{strain2} - \text{strain1}}
This equation allows you to quantify the stiffness of the material within the elastic region, reflecting its ability to resist deformation under stress.Interpret the Result: The resulting value of the modulus of elasticity indicates the substance’s stiffness in the elastic region. An increased elasticity indicates a firmer substance, which is especially important in the choice of components for diverse uses. For instance, recent studies have shown that typical values of modulus for clays with high plasticity range from 0.35 to 32 MPa, while PPS (Polyphenylene Sulfide) demonstrates a significantly higher modulus ranging from 3.30 to 4.00 GPA. Comprehending these values assists in making informed procurement choices regarding selection for specific engineering applications. Additionally, various extensometers, such as clip-on and automated testing options, can significantly impact the accuracy of Young’s Modulus measurement, as highlighted in case studies. As Prof. Mike Ashby observes, ‘The selection of instruments is essential for trustworthy characterization of substances.’ This underscores the importance of selecting appropriate measurement tools in the procurement process.
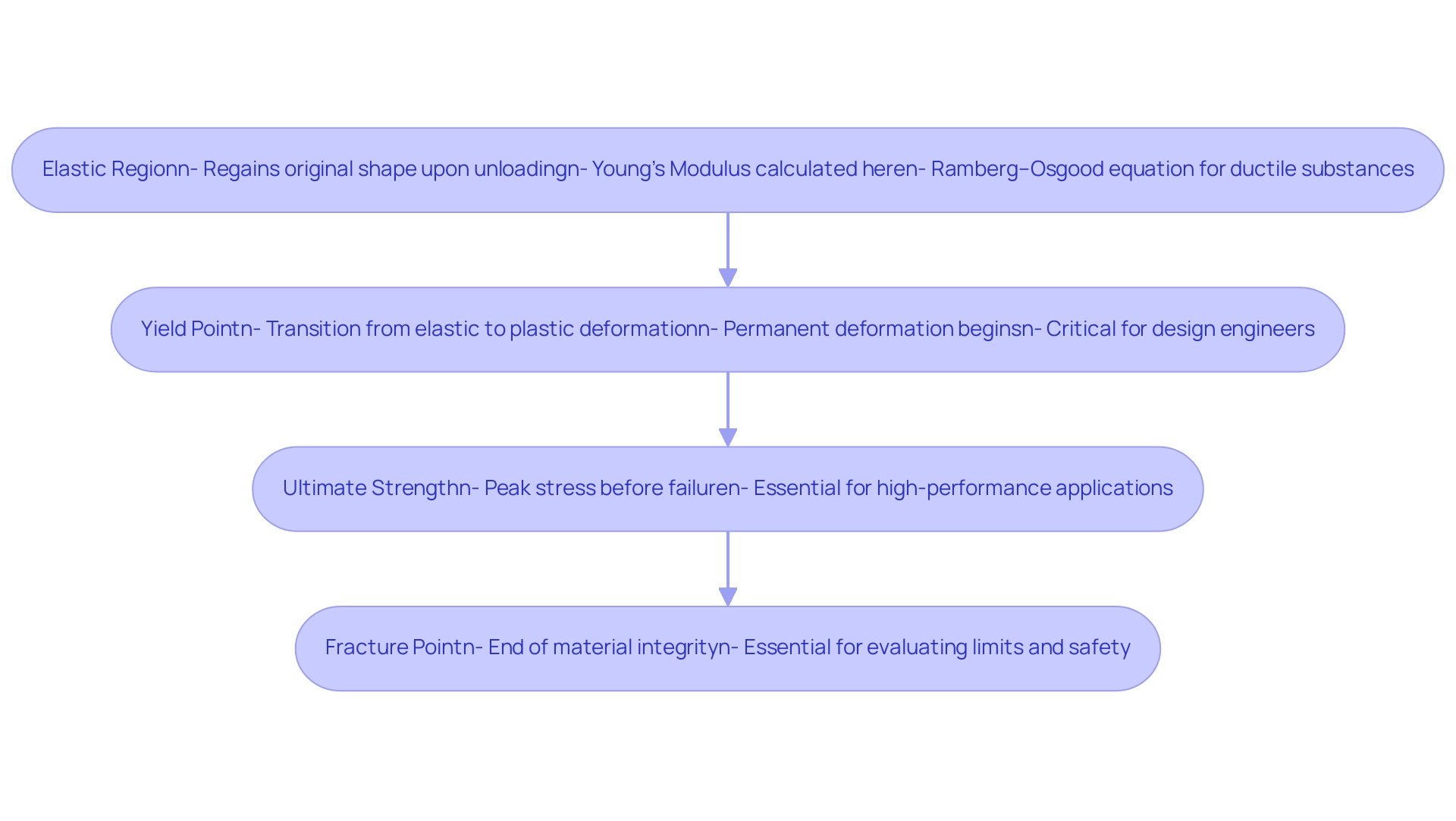
Interpreting the Stress-Strain Curve: Key Features and Their Significance
The stress-strain curve is a pivotal tool in understanding the mechanical properties of materials, featuring several key characteristics:
Elastic Region: This initial segment is represented by a straight line where the substance regains its original shape upon unloading. Young’s Modulus, which quantifies the stiffness of the substance, is calculated within this region, demonstrating how to calculate Young’s modulus from a stress strain curve, and serves as a fundamental parameter in engineering applications. The Ramberg–Osgood equation can be utilized to approximate this curve for ductile substances, providing a more comprehensive understanding of their behavior under stress.
Yield Point: At this critical juncture, the substance transitions from elastic to plastic deformation. Beyond the yield point, any deformation becomes permanent, marking a significant threshold in the behavior of substances that engineers must closely monitor. This is particularly important in the context of the case study titled “Importance of the Strain-Stress Curve,” which highlights how the yield point is crucial for design engineers to determine necessary forces for inducing plastic deformation during fabrication processes.
Ultimate Strength: This is the peak stress that a substance can endure before failure occurs. Comprehending ultimate strength is crucial for applications necessitating high performance under load, ensuring that substances can endure operational demands.
Fracture Point: The end of the substance’s integrity is marked by this point, where it ultimately breaks. Identifying the fracture point is essential for evaluating limits and safety in design.
Expert insights emphasize that careful interpretation of these features is essential. As observed by an engineering specialist, it may not be safe to obtain the first portion to calculate Young’s modulus; there can be some distortion in the initial part due to test machines’ internal dynamics. First be sure that the graph is free from that <.
This highlights the significance of acquiring precise data for dependable engineering analysis, especially regarding how to calculate Young’s modulus from a stress strain curve, which are essential for comprehending stability under stress. By understanding these features, engineers can effectively evaluate performance under various loading conditions, which is crucial in the design and application of substances.
Applications of Young’s Modulus in Engineering and Material Selection
Young’s Elasticity plays an essential role in numerous engineering applications, greatly influencing substance selection and design processes. Its applications include:
- Material Choice: Engineers depend on the elasticity coefficient to determine appropriate substances for structures and components, ensuring they satisfy stiffness criteria.
The modulus of elasticity of carbon steel, for instance, is approximately 200 GPA at room temperature, which decreases to around 150 GPA at elevated temperatures (600°C). This information is vital for procurement managers when assessing performance of resources under different environmental conditions. Moreover, Lacy (1997) derived correlations between dynamic elastic properties and compressional velocity from lab tests of over 400 core samples from the Gulf of Mexico, providing a pertinent real-world example of how these characteristics can be evaluated in practice.
Design Optimization: A thorough comprehension of a substance’s elastic characteristics is essential for engineers, as it helps them understand how to calculate Young’s modulus from a stress strain curve, allowing for the refinement of designs for components that need to withstand particular loads without experiencing significant deformation. As mentioned by Madeira, the rise in modulus in aluminum matrix composites (AMMCs) with added reinforcement mainly stems from increased dislocation density, demonstrating how enhancements can result in better performance. This enhancement is crucial for engineers aiming to create more resilient components.
Failure Assessment: Understanding how to calculate Young’s modulus from a stress strain curve is crucial in forecasting failure points of substances under stress. This predictive capability is essential for ensuring safety in engineering applications, allowing for proactive measures to avoid catastrophic failures. Additionally, the sensitivity of nanocrystalline substances to strain rate changes, influenced by deformation mechanisms and grain size, highlights the importance of considering microstructure in failure analysis.
Quality Control: In manufacturing contexts, the elasticity coefficient serves as a crucial quality assurance metric, ensuring that substances conform to established performance standards. The application of sophisticated tools, like contact extensometers and new non-contact extensometers, improves the precision and consistency of measurements, thereby enabling trustworthy quality evaluations.
In general, the incorporation of elastic modulus in engineering practices not only assists in substance selection but also promotes innovation and safety in design techniques.

Common Questions About Young’s Modulus: Clarifications and Insights
- Distinguishing Young’s Modulus from Other Moduli: Young’s Modulus is a fundamental measure of a substance’s elasticity, specifically explaining how to calculate Young’s modulus from a stress strain curve, which quantifies its ability to deform under tensile or compressive stress. In contrast, shear rigidity assesses the substance’s response to shear stress, while bulk rigidity evaluates its behavior under uniform pressure. Understanding how to calculate Young’s modulus from a stress strain curve provides unique insights into the material’s mechanical behavior, which is essential for informed engineering decisions.
Temperature’s Impact on Elasticity: Indeed, elasticity is not a static value; it varies with temperature. Generally, as temperature rises, the elasticity of materials tends to diminish. This relationship is critical for applications involving thermal variations, as highlighted in a recent study that demonstrated how temperature changes influenced stiffness, particularly in materials subjected to high heat conditions. As noted by Rick Chalaturnyk in his experimental study, the effects of temperature on mechanical properties are significant and warrant careful consideration in design.
- Grasping the Significance of Elasticity: A frequent inquiry emerges: can elasticity be negative? The answer is unequivocally no. The elasticity constant signifies a measure of stiffness; therefore, it is consistently presented as a positive value. This characteristic is fundamental in ensuring consistent behavior predictions of substances under stress.
Influence of Microstructure on Elastic Modulus: The microstructure of a substance is crucial for understanding how to calculate Young’s modulus from a stress strain curve. Factors such as atomic arrangement, grain size, and the presence of defects or inclusions significantly influence elastic properties. For example, substances with a well-organized microstructure generally exhibit higher stiffness, whereas those with considerable defects may demonstrate reduced elastic performance. The recent case study titled ‘Effect of Temperature on Samples’ Stiffness‘ further illustrates this relationship, showing that Young’s modulus decreased with increasing temperature up to 120 °C before increasing again, indicating complex thermal consolidation effects on the substance’s stiffness. Understanding how to calculate Young’s modulus from a stress strain curve is crucial for optimizing material selection and performance in various applications. This study, published on 26 October 2021, underscores the importance of considering temperature effects in mechanical property assessments.

Conclusion
Understanding Young’s Modulus is essential for engineers and procurement managers alike, as it serves as a fundamental indicator of a material’s stiffness and behavior under stress. By mastering the definition, calculation methods, and applications of Young’s Modulus, professionals can make more informed decisions about material selection and design. The ability to accurately interpret stress-strain curves not only aids in determining Young’s Modulus but also reveals critical insights into material performance, including yield points and ultimate strength.
The applications of Young’s Modulus in engineering highlight its significance in:
- Material selection
- Design optimization
- Failure analysis
- Quality control
By leveraging this knowledge, engineers can ensure that components meet performance and safety standards, particularly in industries where durability is paramount. Furthermore, understanding the relationship between Young’s Modulus and factors such as temperature and microstructure enhances the strategic approach to material procurement and application.
In conclusion, mastering the intricacies of Young’s Modulus empowers professionals to optimize material choices and engineering designs, ultimately leading to improved performance and safety in various applications. As the demands on materials continue to evolve, the insights gained from Young’s Modulus will remain a cornerstone of effective engineering practices.




