Blogs

How to Calculate Young’s Modulus from Stress-Strain Curve: A Step-by-Step Guide
Introduction
In the realm of material science and engineering, understanding the fundamental properties of materials is crucial for making informed procurement decisions. Among these properties, Young’s Modulus stands out as a key indicator of stiffness, establishing a direct correlation between stress and strain within the elastic limit of a material.
This article delves into the intricacies of Young’s Modulus, offering a comprehensive guide that encompasses its:
- Definition
- Calculation methods
- Common pitfalls
- Real-world applications across various industries
By equipping procurement managers with the knowledge to accurately assess and utilize this vital property, organizations can enhance their material selection processes, ensuring optimal performance and compliance with industry standards.
Understanding Young’s Modulus: Definition and Importance
Young’s modulus from stress strain curve, also referred to as the stiffness coefficient, is a measure of the rigidity of a substance, quantifying the relationship between stress (force per unit area) and strain (deformation) in the linear elastic region of the stress-strain curve. This property is essential in engineering and materials science because it aids in predicting how components, including high-temperature electrical insulation solutions like Domadia’s Mica Tapes, will deform under various loads. An increased elastic modulus signifies a more rigid substance, which is crucial for uses needing stiffness, like in structural elements of automobiles or electronic gadgets.
By comprehending this concept, procurement managers can make informed decisions when selecting resources based on their mechanical properties and performance requirements, ensuring they choose the best insulation solutions for their specific needs. To explore our range of Mica Tapes and related products such as Electrical Insulation Papers and High-Temperature Fabrics, visit our website or contact our expert team today.
Step-by-Step Calculation of Young’s Modulus from Stress-Strain Data
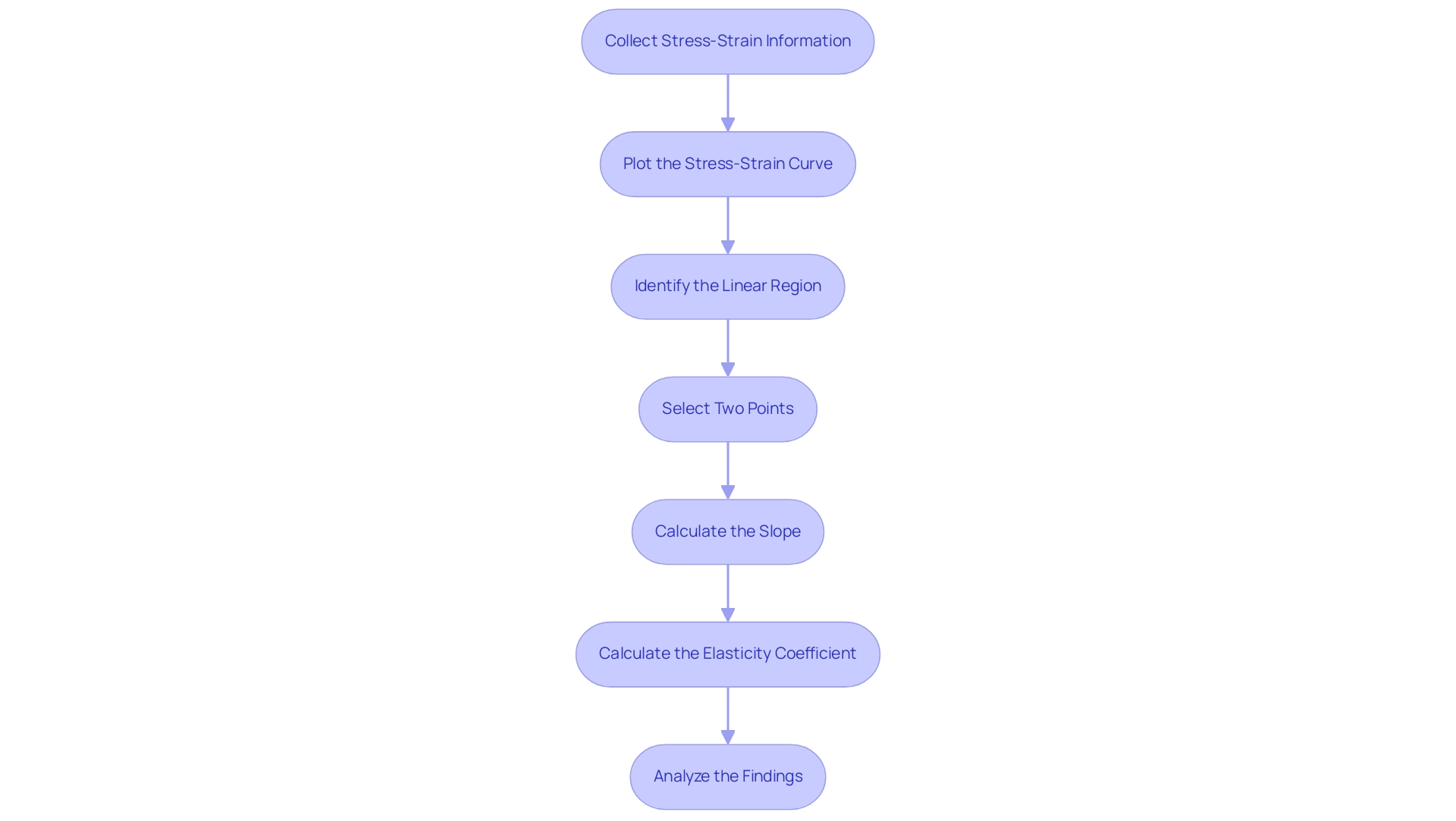
Determining Young’s modulus from the stress strain curve is a crucial ability for procurement managers engaged in selecting substances. As Humberto Villasenor, a Senior Mechanical Engineer, emphasizes, ‘Accurate measurement of Young’s Modulus is crucial for ensuring that the chosen substances meet the required performance criteria.’ Follow this structured approach:
Collect Stress-Strain Information:
Start by acquiring stress-strain information from experimental tests performed on your sample. This information is typically organized in either a tabular format or a graphical representation. You can obtain mechanical property information from sources such as ASTM or manufacturers’ websites.Plot the Stress-Strain Curve:
If your data is in a table, convert it to a graph by plotting stress on the y-axis against strain on the x-axis. This visual representation highlights the substance’s behavior under stress.Identify the Linear Region:
Focus on the linear portion of the stress-strain curve. This segment indicates the elastic behavior of the substance, where it will revert to its original form upon removal of the load. Grasping the difference between strength and stiffness is essential here, as a substance can be strong yet elastic or strong and stiff, but these are distinct qualities.Select Two Points:
Within the linear region, select two distinct points (A and B) and record their corresponding stress and strain values.Calculate the Slope:
The slope of the line joining these two points signifies E. Use the formula:m = \frac{\Delta \text{Stress}}{\Delta \text{Strain}} = \frac{\sigma_B - \sigma_A}{\epsilon_B - \epsilon_A}
Here, ( \sigma ) denotes stress and ( \epsilon ) denotes strain.Calculate the elasticity coefficient:
The slope acquired in the earlier step quantifies the elasticity coefficient, indicating the stiffness of the substance. This value is typically expressed in units such as Pascals (Pa) or Gigapascals (GPA).Analyze the Findings:
Ultimately, evaluate the computed elasticity in relation to your substance selection criteria. Compare your result with industry benchmarks to ensure the material meets the specific requirements of your applications.
By diligently following these steps and utilizing the available resources, you can accurately calculate Young’s modulus from the stress strain curve, facilitating informed decisions in material procurement and enhancing overall project outcomes.
Common Mistakes to Avoid When Calculating Young’s Modulus
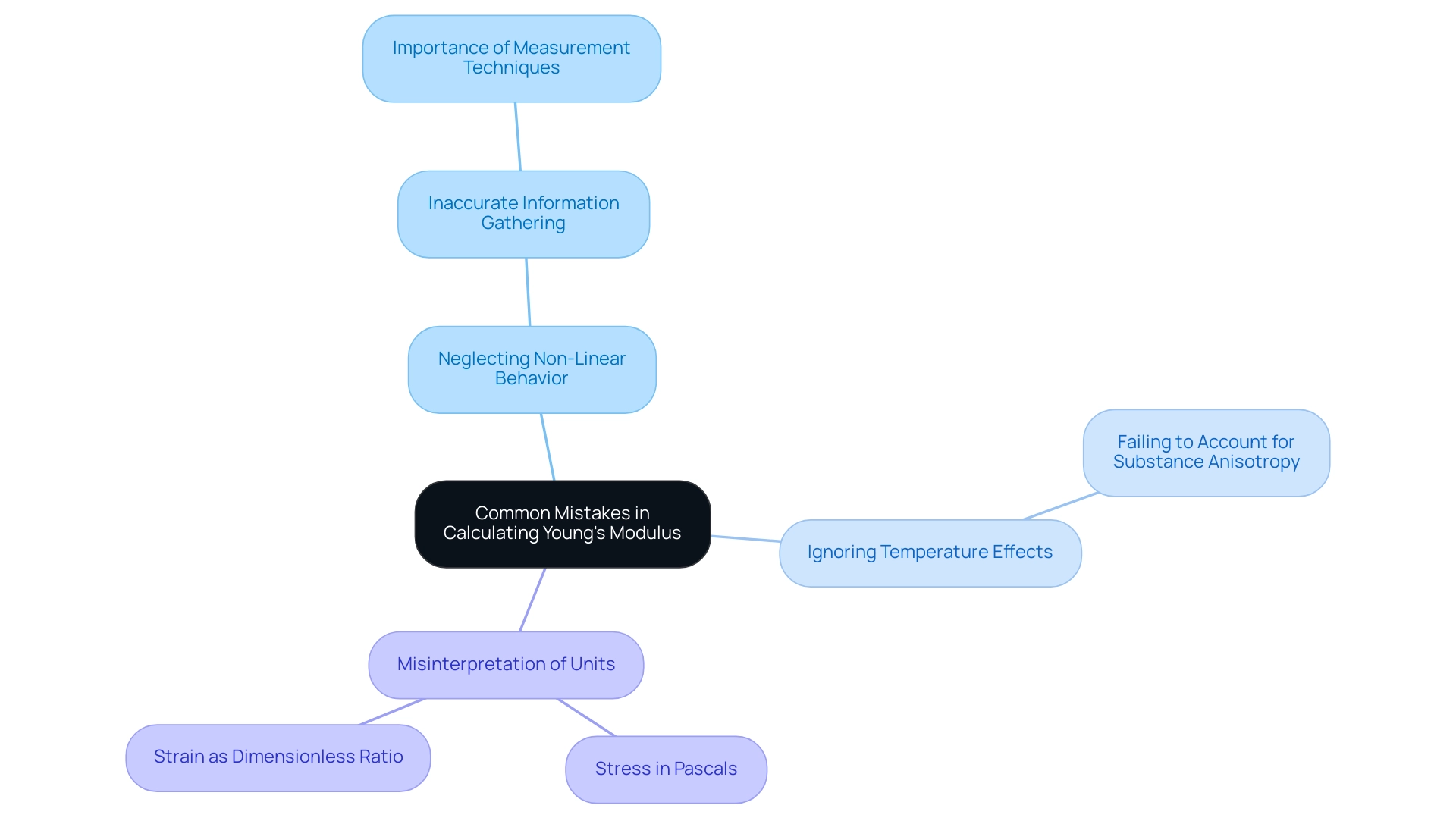
When determining the elastic modulus, it is essential to be cautious about several frequent errors that can result in flawed outcomes:
- Neglecting Non-Linear Behavior: It is imperative to derive Young’s modulus from the stress-strain curve solely from the linear region. Employing information from the plastic deformation stage will lead to significant inaccuracies in the calculations.
Inaccurate Information Gathering: The precision of stress and strain measurements is fundamental. Errors in measurement techniques can drastically skew the calculated Young’s Modulus, highlighting the need for meticulous data collection processes. For instance, Yuan et al. [2015] measured shear and slip using a Gelsight tactile sensor, demonstrating the importance of advanced measurement techniques in obtaining reliable data.
Ignoring Temperature Effects: Material properties can vary with temperature fluctuations. Conduct tests at controlled temperatures and account for any variations to ensure that results reflect true substance behavior.
- Failing to Account for Substance Anisotropy: Many substances, particularly composites and metals, exhibit varying properties based on directional influences. Testing methodologies must consider the anisotropic properties of substances to yield valid results.
- Misinterpretation of Units: It is essential to verify that stress and strain are represented in compatible units during calculations. Stress should be expressed in Pascals, while strain should remain a dimensionless ratio.
By avoiding these pitfalls, the accuracy of determining Young’s modulus from the stress-strain curve can be significantly improved, providing reliable data that is essential for informed substance selection. For example, the elasticity modulus of aluminum is quoted as 69.5 ± 0.3 GPA, underscoring the significance of precise measurements.
As noted by experts in the field, modern measurement techniques, which incorporate sensors and advanced signal processing, are critical to minimizing errors in stress-strain measurements. In a recent study, the relationship for maximum observed surface displacement was applied at each time step during a grasp to retrieve a best-fit value for the aggregate elastic compliance of substances, showcasing the importance of precision in such evaluations.
Additionally, insights from recent case studies, including dimensionality reduction methods in contact mechanics, reveal how a deeper understanding of contact interactions can enhance property estimations, ultimately improving decision-making processes in procurement.
Applications of Young’s Modulus in Material Selection
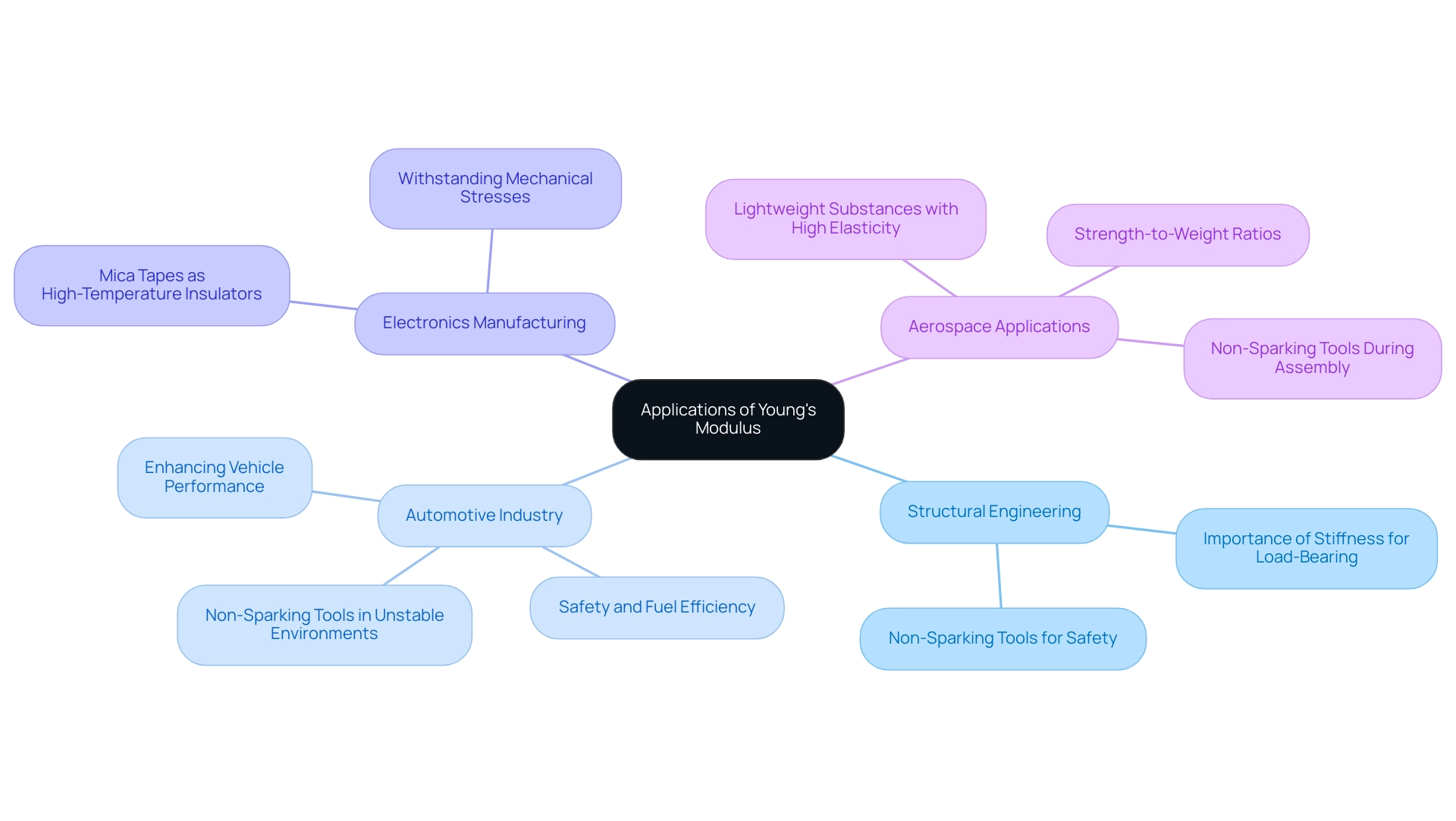
The elasticity coefficient plays an essential role in substance selection across diverse sectors, especially when evaluating high-performance choices such as Domadia’s Mica Tapes and Non-Sparking Tools, which are the top option for non-sparking application needs in explosive settings. Here are some key applications:
Structural Engineering: In construction, substances with elevated stiffness are preferred for load-bearing applications, ensuring stability and durability.
Non-Sparking Tools are essential in explosive environments to prevent ignition risks during structural work.Automotive Industry: Engineers choose substances based on their stiffness to enhance vehicle performance, safety, and fuel efficiency. High elastic modulus substances are frequently utilized in chassis and suspension parts, while Non-Sparking Tools guarantee safe functioning in unstable environments.
Electronics Manufacturing: In electronics, substances must withstand mechanical stresses without deforming. Comprehending the elasticity of materials aids in choosing components that uphold integrity under operational loads. Mica Tapes serve as effective high-temperature electrical insulators, safeguarding sensitive electronics.
Aerospace Applications: Lightweight substances with high elasticity are essential for aerospace components, where strength-to-weight ratios are critical for performance. Employing Non-Sparking Tools during assembly operations further reduces potential dangers in delicate environments.
By incorporating Young’s modulus from the stress-strain curve into resource selection processes, procurement managers can enhance product performance, comply with industry standards, and optimize expenses. To explore our range of Mica Tapes and Non-Sparking Tools, and learn how they can benefit your business, visit our website or contact our expert team today.
Resources for Further Learning about Young’s Modulus
To enhance your comprehension of the elastic constant and its applications, consider exploring the following resources:
- Textbooks on Substance Science: Books such as ‘Substance Science and Engineering: An Introduction’ by William D. Callister provide comprehensive insights into property characteristics, including Modulus of Elasticity.
- Online Courses: Platforms such as Coursera and edX provide classes in substance science and engineering that explore Young’s constant in detail.
- Research Papers: Access academic journals through platforms like Google Scholar to find research papers discussing recent advancements and applications of elasticity in various fields.
- Professional Organizations: Joining organizations such as the Materials Research Society (MRS) or the American Society for Testing and Materials (ASTM) can provide networking opportunities and access to valuable resources.
- Webinars and Workshops: Attend industry webinars and workshops to gain insights from experts and stay updated on best practices in material selection and testing.
By utilizing these resources, you can continue to build your expertise in understanding Young’s modulus from the stress-strain curve and its critical role in material procurement and engineering.
Conclusion
Understanding Young’s Modulus is essential for procurement managers aiming to make informed decisions regarding material selection. This article has explored the definition of Young’s Modulus, its calculation methods, common pitfalls to avoid, and its practical applications across various industries. By mastering the calculation of Young’s Modulus and recognizing the significance of accurate data collection, procurement professionals can ensure they select materials that meet both performance criteria and industry standards.
The importance of Young’s Modulus transcends theoretical knowledge; it directly impacts the effectiveness and safety of materials used in critical applications, from structural engineering to aerospace. By integrating this knowledge into the procurement process, organizations can enhance product performance, reduce risks, and optimize costs, ultimately leading to better outcomes in their projects.
Continued learning and exploration of resources related to Young’s Modulus will further equip procurement managers with the insights necessary to navigate the complexities of material selection. As industries evolve and new materials emerge, staying informed about the latest developments will be paramount in maintaining a competitive edge and ensuring compliance with industry standards.




